鲁晨光中文主页 English Homapage Papers on ArXiv Recent papers about Semantic Information and Statistical Learning
2023年5月于英文Open期刊Entropy发表英文评论文章 :
回顾学习函数和语义信息测度的进化——进而理解深度学习.
Entropy 是MDPI出版公司出版的一个专业期刊,汇集了全球许多对熵和信息感兴趣的作者和读者。这篇是我在Entropy上面发表的第4篇文章。这篇文章经过4位审稿人审稿 (可见编辑重视),一致同意修改发表。主要修改:更改了前两章结构;重要文献和述评集中于Introduction部分;添加了本人研究介绍和实验结果。
下面是中英文版。
| 中文:
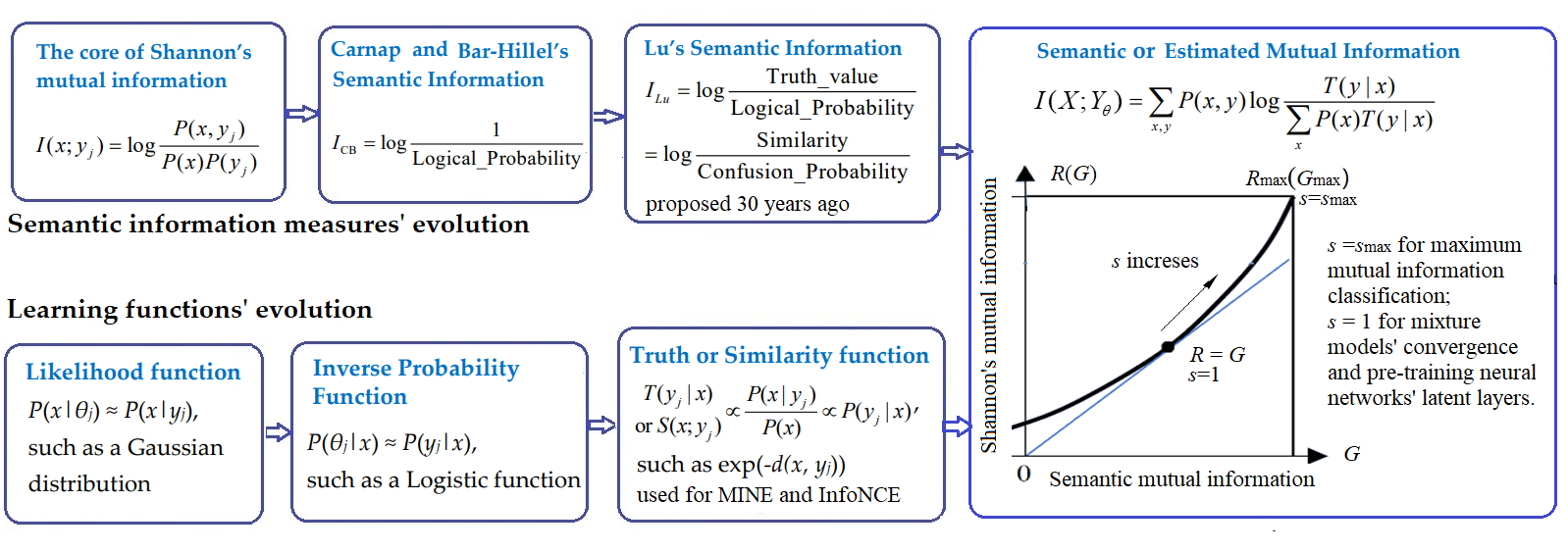
回顾学习函数和语义信息测度的进化——进而理解深度学习(pdf) 摘要: 最近深度学习出现了一股以互信息神经估计(MINE)和信息噪声对比估计(InforNCE)为代表的潮流。在这个潮流中,相似函数和估计互信息分别用作学习函数和目标函数。巧合的是, 估计互信息和笔者30年前提出的语义互信息在本质上完全相同。本文首先回顾了语义信息测度和学习函数的进化史, 然后简单地介绍了笔者的语义信息G理论——包括信息率-保真度函数R(G)(G表示给定的语义互信息,R(G)是信息率-失真函数R(D)的推广)——及其应用于多标签学习,最大互信息分类,和混合模型。然后,文章讨论了:从R(G)函数和G理论的角度,我们应当怎样理解语义互信息和香农互信息之间的关系、构成语义互信息的两个广义熵(模糊熵和覆盖熵)、自动编码器(AutoEncoder)、吉布斯分布(即玻尔茨曼-吉布斯分布)、划分函数…。一个重要结论是:混合模型和有限玻尔茨曼机(RBM)收敛是因为语义互信息最大化的同时香农互信息最小化,使得信息效率G/R接近1。一个潜在机会是:使用高斯信道混合模型预训练深度神经网络(DNN)的隐含层,不需要考虑梯度,从而简化学习。文章也讨论了语义信息测度作为奖励函数(反映控制结果的合目的性)用于强化学习。语义信息G理论有助于解释深度学习, 但是远远不够, 因为深度学习还涉及特征抽取和模糊推理。语义信息论和深度学习相结合应能加速双方发展。
关键词:深度学习,学习函数,语义信息测度, 估计互信息, 最大互信息, 广义熵,相似函数, SoftMax函数,有限玻尔茨曼机。
|
English: Reviewing Evolution of Learning Functions and Semantic Information Measures for Understanding Deep Learning (published on Entropy;Special Issue : The Cornerstone of Machine Learning) Abstract: A new trend in deep learning, represented by Mutual Information Neural Estimation (MINE) and Information Noise Contrast Estimation (InfoNCE), is emerging. In this trend, similarity functions and Estimated Mutual Information (EMI) are used as learning and objective functions. Coincidentally, EMI is essentially the same as Semantic Mutual Information (SeMI) proposed by the author 30 years ago. This paper first reviews the evolutionary histories of semantic information measures and learning functions. Then, it briefly introduces the author’s semantic information G theory with the rate-fidelity function R(G) (G denotes SeMI, and R(G) extends R(D)) and its applications to multi-label learning, the maximum Mutual Information (MI) classification, and mixture models. Then it discusses how we should understand the relationship between SeMI and Shannon’s MI, two generalized entropies (fuzzy entropy and coverage entropy), Autoencoders, Gibbs distributions, and partition functions from the perspective of the R(G) function or the G theory. An important conclusion is that mixture models and Restricted Boltzmann Machines converge because SeMI is maximized, and Shannon’s MI is minimized, making information efficiency G/R close to 1. A potential opportunity is to simplify deep learning by using Gaussian channel mixture models for pre-training deep neural networks’ latent layers without considering gradients. It also discusses how the SeMI measure is used as the reward function (reflecting purposiveness) for reinforcement learning. The G theory helps interpret deep learning but is far from enough. Combining semantic information theory and deep learning will accelerate their development.Keywords: deep learning; learning function; semantic information measure; estimated mutual information; maximum mutual information; generalized entropy; similarity function; SoftMax function; Restricted Boltzmann Machine |