鲁晨光中文主页 English Homapage Papers on ArXiv Recent papers about Semantic Information and Statistical Learning
2023年1月发表的一篇英文文章——《因果确证测度:从辛普森悖论到COVID-19》。下面是中英文对照。
Entropy 是MDPI出版公司出版的一个专业期刊,汇集了全球许多对熵和信息感兴趣的作者和读者。 这篇是我在Entropy上面发表的第3篇文章。第一篇 标题是:《信道确证和预测确证:从医学检验到乌鸦悖论》。第一篇收录于专辑Measring Uncertainty I。本文发表于专辑Measring Uncertainty II。两篇独立成篇,也相互支持。它们如不是贝叶斯确证的终结,也至少是贝叶斯确证绕不过去的里程碑。本文首次提出将贝叶斯确证理论或研究者划分为增量派和归纳派,笔者支持归纳派,但是这种归纳重视反例的否定意义,兼容Popper的证伪理论。
| 中文:
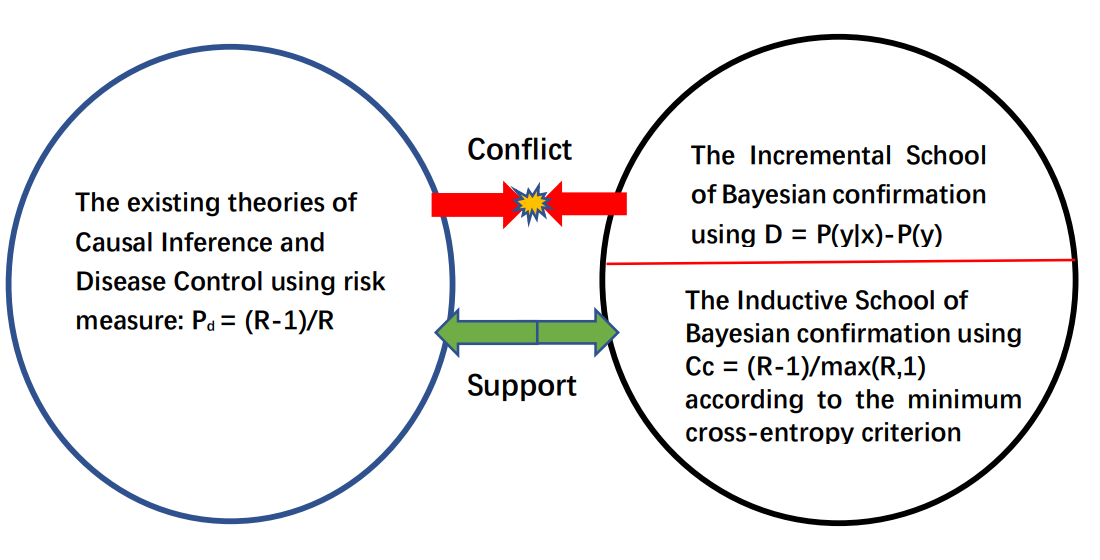
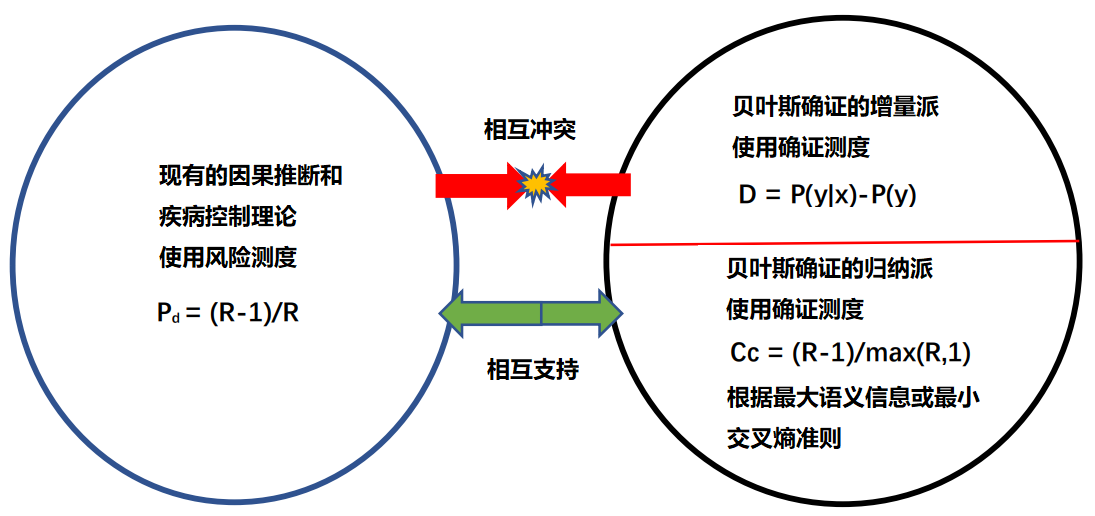
因果确证测度:从辛普森悖论到COVID-19(PDF) 摘要:用统计数据比较两种原因对结果的影响时,如果我们得到的合并结论和分组结论相反,这被称之为辛普森悖论(英文是Simpson Paradox, 缩写为SP)。现在流行的因果推断理论(英文是Popular Causal Inference Theory, 缩写为PCIT)通过去混杂影响,使合并结论和分组结论一致,从而消除SP。PCIT使用相对风险差Pd=max(0,(R-1)/R)作为反映因果关系的概率(R=正例比例/反例比例),而哲学家Fitelson用确证测度D(D=后验概率-先验概率)评价因果关系强度。Fitelson得出结论:从贝叶斯确证理论看,我们无需考虑混杂影响,直接接受合并结论就行了。为了消除PCIT和贝叶斯确证之间的矛盾,作者使用语义信息方法推导出因果确证测度Cc=R-1)/max(R,1)。这一测度很像Pd, 但是具有归一化性质(在-1和1之间变化)和原因对称性(相反原因会使得确证度为负)。Cc特别适合原因抑制结果(比如疫苗抑制感染)的情况(确证度是负的)。文中提供的一些例子(关于肾结石治疗和COVID-19)表明Pd和Cc比D更加合理,Cc比Pd更加有用。Pd和Cc的合理性反过来支持了贝叶斯确证的归纳派。 关键词:因果确证;贝叶斯确证;因果推理,语义信息测度,交叉熵,辛普森悖论,风险测度
|
English: Causal Confirmation Measures: From Simpson’s Paradox to COVID-19
(published on
Entropy Special Issue
Measuring Uncertainty II) Abstract: When we compare the influences of two causes on an outcome, if the conclusion from every group is against that from the conflation, we think there is Simpson’s Paradox. The Existing Causal Inference Theory (ECIT) can make the overall conclusion consistent with the grouping conclusion by removing the confounder’s influence to eliminate the paradox. The ECIT uses relative risk difference Pd = max(0, (R − 1)/R) (R denotes the risk ratio) as the probability of causation. In contrast, Philosopher Fitelson uses confirmation measure D (posterior probability minus prior probability) to measure the strength of causation. Fitelson concludes that from the perspective of Bayesian confirmation, we should directly accept the overall conclusion without considering the paradox. The author proposed a Bayesian confirmation measure b* similar to Pd before. To overcome the contradiction between the ECIT and Bayesian confirmation, the author uses the semantic information method with the minimum cross-entropy criterion to deduce causal confirmation measure Cc = (R − 1)/max(R, 1). Cc is like Pd but has normalizing property (between −1 and 1) and cause symmetry. It especially fits cases where a cause restrains an outcome, such as the COVID-19 vaccine controlling the infection. Some examples (about kidney stone treatments and COVID-19) reveal that Pd and Cc are more reasonable than D; Cc is more useful than Pd. Keywords: causal confirmation; Bayesian confirmation; causal inference; semantic information measure; cross-entropy; Simpson’s Paradox; COVID-19; risk measures |